第 6 章运算方法和运算部件

byml2024-06-25数字系统设计基础

第一讲基本运算部件

算数逻辑单元（ALU）没有统一的结构，可以根据功能进行设计。

Note

从需求角度，硬件的设计会去符合软件的需求

高级程序设计中所涉及到的运算

基本类型

基本数据类型：无符号数、带符号整数、浮点数、位串、字符（串）
基本运算类型：算数（加减乘除）、按位（与或非）、逻辑、移位（左移右移）、扩展和截断、匹配

底层实现

将各类表达式编译（转换）为指令序列
计算机直接执行指令来完成运算

底层需要提供哪些运算来满足这些运算需求？

整数算术运算、浮点数算数运算
按位、逻辑、移位、位扩展和位截断

其中逻辑运算、移位、扩展和截断等指令实现较为容易，而算术运算指令较难实现。可以使用多路选择器实现输出对应功能的效果。

指令集中涉及的运算

RISC-V 指令系统提供的运算类指令

定点数算数运算
- 带符号整数：取负、符号扩展、加减乘除、算术移位
- 无符号整数：0 扩展、加减乘除
逻辑运算
- 逻辑操作：与或非
- 逻辑移位：逻辑左移、逻辑右移
浮点数算数运算：加减乘除

串行进位加法器

通过组合逻辑电路实现：[[第 3 章组合逻辑电路#串行进位加法器/行波进位加法器|串行进位加法器]]

module FA(
    input x, y, cin,
    output f, cout
);
    assign f = x ^ y ^ cin;
    assign cout = (x & y) | (x & cin) | (y & cin);
endmodule

并行进位加法器（CLA 加法器）

通过组合逻辑电路实现：[[第 3 章组合逻辑电路#超前进位加法器|并行进位加法器]] 通过展开和推导，搭建出可根据输入，计算出先行进位的 CLU 部件

先行进位计算过程

构造：

进位生成函数： $G_{i} = X_{i} Y_{i}$
进位传递函数： $P_{i} = X_{i} + Y_{i}$ （或 $P_{i} = X_{i} \oplus Y_{i}$ ）

得到全加逻辑方程： ${\begin{cases} S_{i} = X_{i} \oplus Y_{i} \oplus C_{i} \\ C_{i} = G_{i} + P_{i} C_{i - 1} \end{cases} (i = 1, 2, \dots, n)$ 将 $C_{2}, C_{3}, \dots, C_{n}$ 逐级展开，即可实现仅用输入表示出进位

局部（单级）先行进位加法器

思路：组内并行，组间串行

局部先行进位加法器（PartialLookahead Adder）：全使用先行进位加法器的成本太高（需要在 CLU 中使用太多的逻辑部件），因此使用 N 位先行进位加法器，合成一个大加法器。最长延迟 = GP 计算 + CLU 中最长的逻辑表达式计算 + S 计算

两级/多级先行进位加法器

思路：组内并行，组间并行

当前最常用的方法，通过 BCLU 部件计算出组间进位，使计算进一步加速。输入接入 BCLU，BCLU 的输出逐级上传，计算出组间进位，然后下传后开始并行计算加法。最长延迟 = GP 计算 + CLU 中最长的逻辑表达式计算（除了最顶层，上行和下行均要计算，上行算的是最高位进位，下行算的是每一位具体的进位）+ S 计算

n 位带标志加法器

需求：增加运算结果的标志信息

判断是否溢出
比较大小标志：
溢出标志 $O F = C_{n} \oplus C_{n - 1}$
符号标志 $S F = F_{n - 1}$
零标志 $Z F = 1$ 当且仅当 $F = 0$ （实现是将所有输出接入一个或非门）
进位/借位标志位 $C F = C_{o u t} \oplus C_{i n}$

算数逻辑部件（ALU）

通过选择器控制 ALU 处于的工作状态。 ALU 具有如下功能：

加减：add, sub, addu, subu
逻辑：or
比较：slt, sltu

	无符号整数	有符号整数
加法
减法

$A \oplus 1 = \overset{―}{A}$ 且 $A \oplus 0 = A$ ，可用异或门对加减法中 $B$ 的状态进行处理。

标志位

溢出标志 OF

符号位进位与最高数值位进位相同，则无溢出，即 $O F = C_{n} \oplus C_{n - 1}$

符号位进位（最高位进位）	最高数值位进位（次高位进位）	加数类型	溢出状态 OF
0	0	两个正数一正一负	0
0	1	两个正数	1
1	0	两个负数	1（负+负出现了正数）
1	1	两个负数	0（符号位保持了不变）

进位/借位标志 CF

$C F = C_{i n} \oplus C_{o u t}$

加减标志 $C_{i n}$	输出 $C_{o u t}$	进位/借位状态 CF
0 (加法)	0	0 无进位
0（加法）	1	1 进位
1（减法）	0	1 借位
1（减法）	1	0 无借位

减法的借位

(A - B) \mod 2^{n} = ([A] + [B]_{补}) \mod 2^{n} = (A - B + 2^{n}) \mod 2^{n}

若 $A > B$ ，则不借位，此时自然溢出
若 $A < B$ ，则借位，此时不会溢出

使用减法进行大小比较

使用减法来比较大小：

有符号整数：
- 若 $A > B$ ，则 $A - B$ 的 $O F = S F (O F \oplus S F = 0)$
- 若 $A < B$ ，则 $A - B$ 的 $O F \neq S F (O F \oplus S F = 1)$
无符号整数：
- 若 $A > B$ ，则 $A - B$ 的 $C F = 0$
- 若 $A < B$ ，则 $A - B$ 的 $C F = 1$

原码加减运算

原码加减用于浮点数位数运算，原理如下：

符号位和数值位分开处理
仅对数值部分进行加减运算，符号位起到判断和控制作用规则如下：
比较两数符号，对加法实行“同号求和，异号求差”的运算，对减法实行“异号求和，同号求差”的运算
求和：数值位相加，和的符号取被加数的符号。若最高位产生进位，则结果溢出。
求差：被减数加上减数的补码。
- 差的符号位

优化：

累算部分积，而不是最终累加
存数改为高位在右，左移改右移
只用最高 n 位长度的加法器滑动即可
遇到 0 的时候，直接右移（在二进制下，遇 0 右移，遇 1 直接加）

电路实现

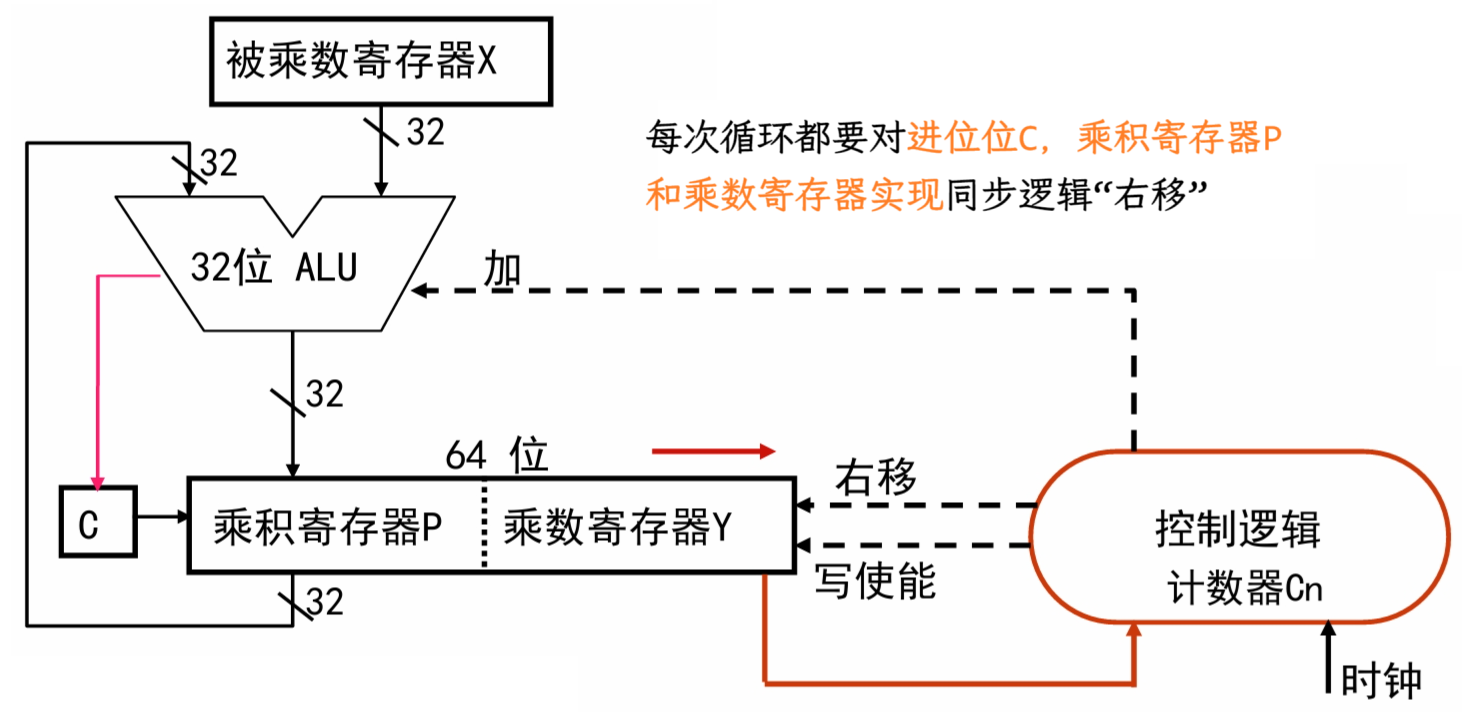
被乘数寄存器 X：存放被乘数
乘积寄存器 P：开始置初始部分积 $P_{0} = 0$ ；结束时，存放的是64位乘积的高32位
乘数寄存器 Y：开始时置乘数；结束时，存放的是64位乘积的低32位
进位触发器 C：保存加法器的进位信号
循环次数计数器 Cn：存放循环次数。初值32，每循环一次，Cn减1，Cn=0时结束
ALU：乘法核心部件。在控制逻辑控制下，对 P 和 X 的内容“加”，在“写使能”控制下运算结果被送回 P，进位位在 C 中

原码的乘法运算

用于浮点数尾数乘运算。符号与数值分开处理，积的符号通过符号位异或得到，数值部分用无符号乘法计算。

两位乘法

与一位乘法不同，两位乘法每次取乘数的两位进行处理，因此可以将运行时间降低到原来的一半：

情况	迭代公式	进行操作
00	$P_{n + 1} = 2^{- 2} P$	直接移两位
01	$P_{n + 1} = 2^{- 2} (P + X)$	先 $+ X$ ，移两位
10	$P_{n + 1} = 2^{- 2} (P + 2 X)$	先 $+ X + X$ ，移两位
11	$P_{n + 1} = 2^{- 2} (P + 3 X) = 2^{- 2} (P_{i} - X) + X$	先 $+ [X]_{补}$ ，移两位，再 $+ X$

若 $被除数 = 0$ 且 $除数 \neq 0$ ，或定点整数除法时 $| 被除数 | < | 除数 |$ ，则商为0，不再继续
若 $被除数 \neq 0$ 、 $除数 = 0$ ，则发生“除数为0”异常（浮点数时为∞）若浮点除法被除数和除数都为0，则有些机器产生一个不发信号的NaN，即“quiet NaN”
当 $被除数和除数都 \neq 0$ ，且 $商 \neq 0$ 时，才进一步进行除法运算。计算机内部无符号数除法运算与手算一样，通过被除数（中间余数）减除数来得到每一位商够减上商1；不够减上商0（从msb→lsb得到各位商）基本操作为减（加）法和移位，故可与乘法合用同一套硬件两个n位数相除的情况：

定点正整数（即无符号数）相除：在被除数的高位添 n 个 0
定点正小数（即原码小数）相除：在被除数的低位添加 n 个 0。这样，就将所有情况都统一为：一个 2n 位数除以一个 n 位数。

电路实现

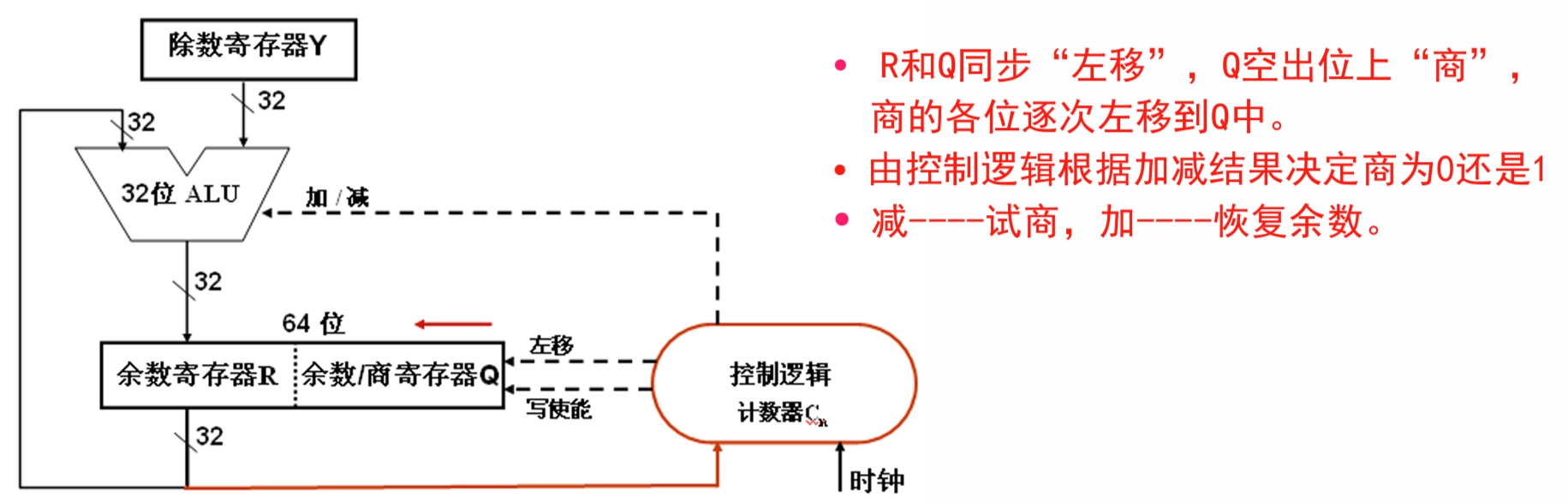
除数寄存器 Y：存放除数。
余数寄存器 R：初始时高位部分为高32位被除数；结束时是余数。
余数/商寄存器 Q：初始时为低32位被除数；结束时是32位商。
循环次数计数器 Cn：存放循环次数。初值是32，每循环一次，Cn减1，当Cn=0时，除法运算结束。
ALU：除法核心部件。在控制逻辑控制下，对于寄存器 R 和 Y 的内容进行“加/减”运算，在“写使能”控制下运算结果被送回寄存器 R。

不恢复余数法（加减交替法）

根据恢复余数法(设 $B$ 为除数， $R_{i}$ 为第 $i$ 次中间余数)，有：

若 $R_{i} < 0$ ,则商上“0”，把先做加法恢复余数再移位，改为直接在下一步做加法
若 $R i >= 0$ ,则商上“1”，不需恢复余数由此省去了恢复余数的过程。但注意：最后一次上商为“0”的话，需要“纠余”处理，即把试商时被减掉的除数加回去，恢复真正的余数。

带符号数除法

原码除法
- 商符和商值分开处理
- 商的数值部分由无符号数除法求得
- 商符由被除数和除数的符号确定：同号为0，异号为１
- 余数的符号同被除数的符号
补码除法
- 方法1：同原码除法一样，先转换为正数（类似原码表示），先用无符号数除法，然后修正商和余数。
- 方法2：直接用补码除法，符号和数值一起进行运算，商符直接在运算中产生。

第 6 章运算方法和运算部件

第一讲基本运算部件

高级程序设计中所涉及到的运算

基本类型

底层实现

指令集中涉及的运算

串行进位加法器

并行进位加法器（CLA 加法器）

局部（单级）先行进位加法器

两级/多级先行进位加法器

n 位带标志加法器

算数逻辑部件（ALU）

第二讲定点数运算

定点数加减运算

补码加减运算

n 位整数加减运算器

标志位

溢出标志 OF

进位/借位标志 CF

使用减法进行大小比较

原码加减运算

移码加减运算

定点数乘法运算

无符号数的乘法运算

电路实现

原码的乘法运算

两位乘法

补码乘法运算

定点数除法运算

除前预处理

电路实现

不恢复余数法（加减交替法）

带符号数除法

第三讲浮点数运算

目录

第 6 章 运算方法和运算部件

目录

第 6 章运算方法和运算部件