Lecture 2 - Classification

byml2024-08-05CVCS231n

Problem: Semetic Gap（语义鸿沟）人类视觉看到的是色彩信息，而计算机看到的是 RGB 色值构成的矩阵
Challenges:
- Viewpoint variation: 同一个物体，从不同视角观察，像素矩阵可能完全不同
- Illumination：同一物体，在不同的光照条件下，像素矩阵可能完全不同
- Deformation：同一物体，可能发生形变（比如姿势的改变），导致像素矩阵的差异
- Occlution：当物体被部分遮挡时，应该如何准确识别
- Background Clutter：混乱或与前景相似的背景会导致前景的物体难以被辨认
- Intraclass variation：同一种物体，存在个体差异
Data-Driven Approach：通过数据集的训练而非硬编码，让算法能够处理分类任务
1. 收集“图像-标签”数据集
2. 使用机器学习训练一个分类器
3. 使用新的图片评估分类器的性能

Nearest Neigbour

训练过程：记忆所有的“图像-标签”对
预测过程：找到和数据图像最相似的图像对应的标签

测试数据集

CIFAR10

50,000 训练集
10,000 测试集

Distance Metric（距离度规）

两个图片之间的相似程度的衡量方式

L1: Manhattan Distance

d_{1} (I_{1}, I_{2}) = \sum_{p} | I_{1}^{p} - I_{2}^{p} |

基于曼哈顿距离的 Nearest Neigbour 分类算法

import numpy as np
class NearestNeibour:
    def train(self, X, y):
        self.Xtr = X
        self.ytr = y
    def predict(self, X):
        num_test = X.shape[0]
        Ypred = np.zeros((num_test,))
        for i in range(num_test):
            distance = np.sum(np.abs(self.Xtr-X[i,:]), axis=1)
            min_idx = np.argmin(distance)
            Ypred[i] = self.ytr[min_idx]
        return Ypred

训练复杂度： $O (1)$
推理复杂度： $O (n)$ 训练用时少而推理用时大，不太符合预期

L2: Euclidean Distance

d_{2} (I_{1}, I_{2}) = \sqrt{\sum_{p} (I_{1}^{p} - I_{2}^{p})^{2}}

K-Nearest Neigbour

当前输入的图像所属的标签，是离它最近的 k 个点中出现次数最多的标签。

Limitation

距离度规均无法很好的表征图像之间的感知差异度（像素差异度和感知差异度之间并不具有一致性）
维度限制：为了保证 KNN 的效果，我们希望训练集能够密集地覆盖整个空间（即总能找到合适的邻居），这就导致需要的样本数据量会随着数据维度的增加呈指数增加，使构建训练集变得困难。

Hyperparameters

训练集、验证集和测试集

将数据集划分为 training set, validation set 和 test set 三部分：

使用 training set 进行训练
使用 validation set 调整超参数
使用 test set 评估算法效果

测试集

测试集的使用要非常慎重，因为根据测试集的反馈再调整超参数，就容易准确率虚高的情况。

交叉验证

将数据集划分为 training set 和 test set 两部分：

将 training set 再划分为若干个 fold，每次训练，挑选出一个 fold 作为 validation set，然后用其他 fold 进行训练，根据 validation set 的结果调整超参数
最后使用 test set 评估算法效果缺点是需要多次训练，开销较大

Linear Classification

Paramatric Approch

Paramatric model: 输出是输入 $x$ 和参数 $W$ 的函数，即 $f (x, W)$ ，模型将训练得到的知识存储于参数 $W$ 中
在训练过程中，模型学习得到 $W$ ；而在推理过程中，模型就可以直接使用 $W$ 和新的输入 $x$ ，从而能够做到保证效果的同时占用更少的资源。
不同的深度学习模型，实际上就是对应着不同结构的 $f$

Linear Classification Model

当 $f (x, W) = W x + b$ 时，模型就是最简单的线性分类模型。
假如输入是一张 $32 \times 32$ 的 RGB 图片，任务是将这张图片分到 $10$ 种类别中的一类里面，则 $x$ 会是一个 $32 \times 32 \times 3 = 3072$ 维的向量，而 $W$ 会是一个 $10 \times 3072$ 的矩阵， $b$ 是一个 $10$ 维的向量，最终输出的结果就会是一个 $10$ 维的向量。
通过可视化训练后的权重 $W$ 发现，权重矩阵中存储的内容是一种类似“典型模板”的图片，即当以这张图作为输入，输出向量中对应该分类的数值取到了最大值
- 权重 $W$ 的每一行，都对应了输入和一种分类的输出结果关系（例如，第一分类输出值是 $W$ 的第一行和输入向量的点乘），因此，可以根据这个关系将权重矩阵第一行还原得到“典型模板”
- 单层的分类器只能存储一个“典型模板”，这也解释了其在分类问题上所存在的局限性
从另一个角度出发，线性分类器的工作是将高位空间中的点通过决策边界分割到不同的类别中

Limitation

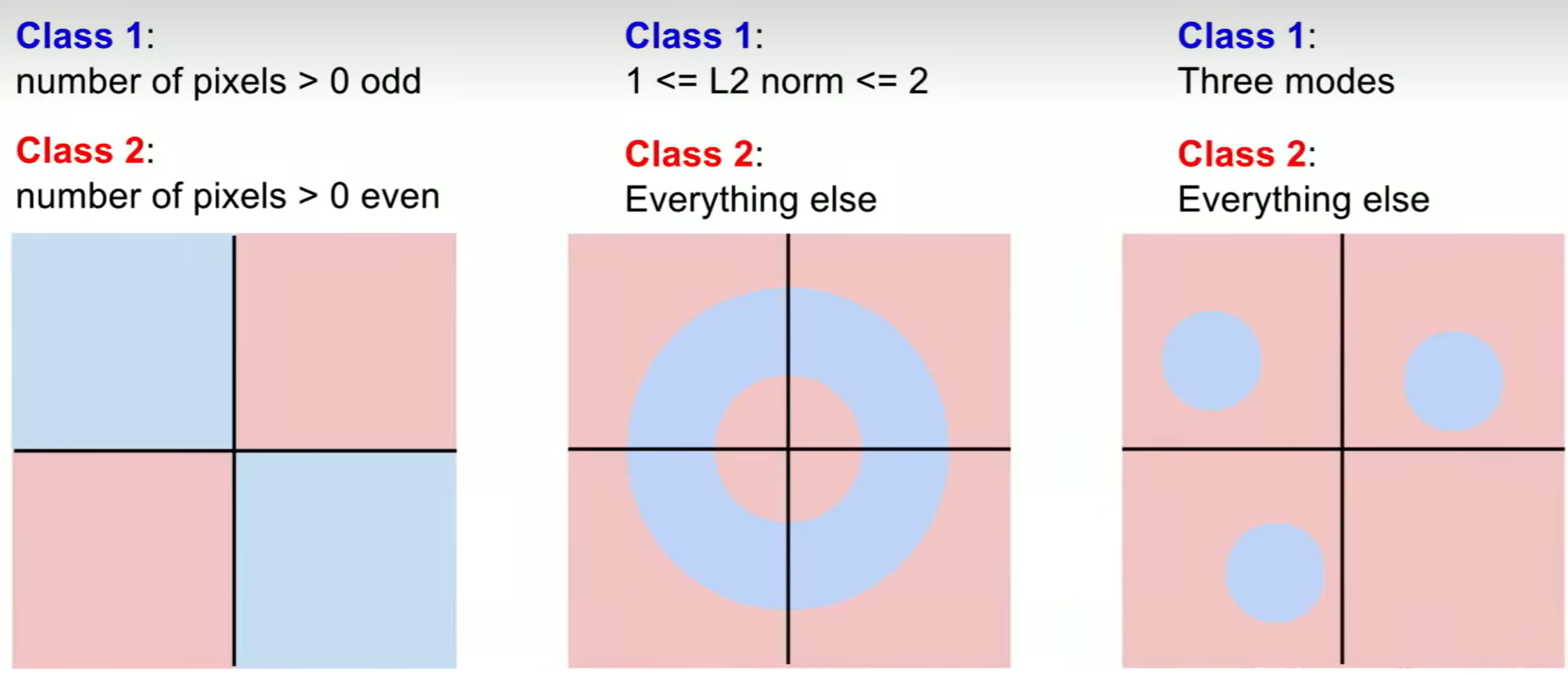
具有多种“典型模板”的问题（反映在图像上就是同一个类别出现“孤岛”的情况），线性分类模型无法很好的解决

Lecture 2 - Classification

目录