Lecture 3 - Loss Function and Optmizatoin

byml2024-08-05CVCS231n

Loss Function

损失函数的作用是用来量化权重矩阵 $W$ 的好坏
假设存在数据集： ${(x_{i}, y_{i})}_{i = 1}^{N}$ ，其中 $x_{i}$ 是第 $i$ 个输入， $y_{i}$ 是第 $i$ 个输入对应的标签，则损失函数 $L$ 可表示为：

L = \frac{1}{N} \sum_{i = 1}^{N} L_{i} (f (x_{i}, W), y_{i})

Muliple SVM Loss

设 $s = f (x_{i}, W)$ ，则：

\begin{aligned} L_{i} & = \sum_{j \neq y_{i}} {\begin{cases} 0 & if s_{y_{i}} \geq s_{j} + 1 \\ s_{j} - s_{y_{i}} + 1 & otherwise \end{cases} \\ = \sum_{j \neq y_{i}} max (0, s_{j} - s_{y_{i}} + 1) \end{aligned}

其中的 $1$ 是设定的 safety margin（安全距离），即正确选项和非正确选项之间应至少保持 $1$ 的距离
据其形状，这种损失函数也被称作“Hinge Loss”

初始损失

通过随机初始化 $W$ 后，初始运行结果可能是 $s$ 的每一维都是相近的接近 $0$ 的数，此时损失函数 $=$ 类别总数 $- 1$ ，可以用来验证算法正确性（DEBUG）

Regularization

通过引入 Regularization Loss Fucntion $R (W)$ ，鼓励模型选择更加简单的函数（软约束），以避免过拟合：

L (W) = \frac{1}{N} \sum_{i = 1}^{N} L_{i} (f (x_{i}, W), y_{i}) + λ R (W)

其中的 $λ$ 是用来调整损失函数和正则函数影响大小的超参数，需要根据实际问题进行调整。

Occam's Razor

Among competing hypothese, the simplest is the best.

常用的正则函数有：
- L2 regularization: $R (W) = \sum_{k} \sum_{l} W_{k, l}^{2}$
- L1 regularization: $R (W) = \sum_{k} \sum_{l} | W_{k, l} |$
- Elastic net (L1+L2): $R (W) = \sum_{k} \sum_{l} (β W_{k, l}^{2} + | W_{k, l} |)$
- Max norm regularization
- Dropout
- Fancier: Batch regularization, stochastic depth

L1 和 L2 的对比

L1 和 L2 相比，L1 会更倾向于选择稀疏矩阵，而 L2 更倾向于选择分布均匀的矩阵。例如，输入 $x = [1, 1, 1, 1]$ ，权重 $w_{1} = [1, 0, 0, 0], w_{2} = [0.25, 0.25, 0.25, 0.25]$ ，此时 $w_{1}^{T} x = w_{2}^{T} x = 1$ ，且 $R_{L_{1}} (w_{1}) = R_{L_{1}} (W_{2})$ ，但 $R_{L_{2}} (w_{1}) > R_{L_{2}} (w_{2})$ ，可以看出，L2 更倾向于选择分布均匀的矩阵 $w_{2}$ 。

Softmax Loss (Multinomial Logistic Regression)

通过 $s = f (x_{i}, W)$ 来计算得分的概率分布：

P (Y = k | X = x_{i}) = \frac{e^{s_{k}}}{\sum_{j} e^{s_{j}}}

这样处理使得选择任意类别的概率 $s_{k} \in [0, 1]$ ，且所有类别的选择概率和 $\sum_{k} s_{k} = 1$ ，这使得经过处理后的 $s$ 具有了可解释性。
我们希望 $P (Y = y_{i} | X = x_{i})$ 尽量接近 $1$ ，即最大化 $\log P (Y = y_{i} | X = x_{i})$ ，或最小化 $- \log P (Y = y_{i} | X = x_{i})$ ，因此可以得到：

L_{i} = - \log P (Y = y_{i} | X = x_{i}) = - \log (\frac{e^{s_{y_{i}}}}{\sum_{j} e_{j}^{s}})

Softmax 损失函数也被称作“Cross-entropy Loss”

初始损失

通过随机初始化 $W$ 后，初始运行结果可能是 $s$ 的每一维都是相近的接近 $0$ 的数，因此 $P (Y = y_{i} | X = x_{i}) \approx \frac{1}{类别总数}$ ，故 $L_{i}$ 近似为 $\log (类别总数)$ ，可以用来判断算法准确性（DEBUG）

对比 SVM Loss 和 Softmax Loss，前者只需非正确类别的分数低于正确类别一定距离，就判定为无损失；而后者总是希望将所有概率密度都堆积在正确类别上，这会导致其希望正确类别的分数趋于正无穷，而错误类别的分数趋于负无穷，在有限精度下无法使损失函数真正为 0

Optimization

Optimization 的目的就是为了找到使得损失函数 $L$ 最小的权重矩阵 $W$
完整的损失函数的一般形式：

L (W) = \frac{1}{N} \sum_{i = 1}^{N} L_{i} (f (x_{i}, W), y_{i}) + λ R (W)

其中的 $x_{i}, y_{i}, N$ 是与数据集有关的量， $f, L_{i}, λ, R$ 是人为设定的超参数（或函数）， $W$ 是唯一变量
- 实际问题中， $f$ 可能非常复杂，有可能是复杂函数，也有可能是多层神经网络，很难直接求导
- 因此，在实际问题中，往往使用迭代法去求解损失函数的最小值

Gradient（梯度）

多元函数的梯度是一个向量，其每一维度的值是函数对相应元的偏导数。某点处的梯度指向的是多维空间中，函数增速最快的方向。因此，负梯度指向的方向就是函数减少最快的方向。
梯度也是多元函数在某点处的线性一阶近似。

有限差分法

通过有限差分计算梯度，就是在利用偏导数的极限定义

\frac{\partial F}{\partial x_{i}} = lim_{Δ x \to 0} \frac{F (x_{1}, \dots, x_{i} + Δ x, \dots, x_{n}) - F (x_{1}, \dots, x_{i}, \dots, x_{n})}{Δ x}

有限差分法的时间复杂度为 $计算 F 的时间 \times 变量元数$ ，这在 F 非常复杂、变量很多的实际情况下，极其低效

微积分

通过求解梯度的解析式，可以极大提高计算梯度的精度和效率，直接根据输入计算一次函数求得梯度

使用有限差分验证解析式

将通过有限差分法得到的梯度与使用自己推导出来的解析式计算出来的梯度进行对比，如果偏差过大，则意味着可能出现了推导错误

Gradient Descent（梯度下降）

while True:
    weights_grad = evaluate_gradient(loss_fun, data, weights)
    weights += - step_size * weights_grad

step_size 或者也称作 learning_rate，是每次沿着负梯度方向前进的距离，是一个非常重要的超参数

Stochastic Gradient Descent

在实际问题中，数据集可能会非常大，这将导致计算损失函数变得非常慢。因此，我们会采用随机采样的方式，获取估计的梯度，据此进行梯度下降

while True:
    data_batch = sample_training_data(data, minibatch_size)
    weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
    weights += - step_size * weights_grad

minibatch_size 即为采样数，是一个超参数，一般取 32、64、128、256 等

Feature

对于某些问题，我们无法直接对其进行线性分类，但我们可以通过先将问题转化为可线性分类的问题，再进行处理的方式使其可以应用线性分类解决。

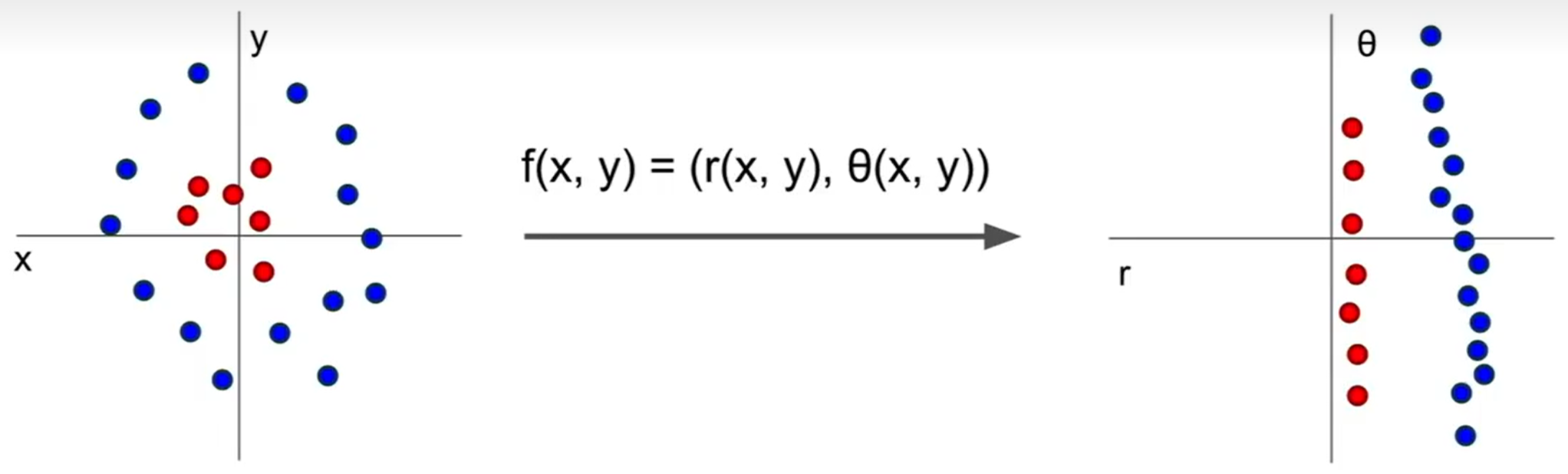
Histogram of Oriented Gradiants (HoG)

定向梯度直方图：模仿人类识别物体时更加关注物体边缘，提出通过计算边缘方向的方式，捕获图像特征
研究者将图像划分成 $8 \times 8$ 的区域，然后在每个区域中用直方图统计沿各个方向的像素出现频次
如果将图像分成 $30 \times 40$ 个区域，那么最终输入线性分类器的是一个 $30 \times 40 \times 9$ 的向量（其中的 $9$ 表示直方图统计的设定的 $9$ 个方向）

Bag of Words

模仿 NLP 中的词袋模型，先将图片切块，通过 KNN 获取若干个聚类中心，将这些中心标记为“词”，再将图片根据这些词取直方图，最后使用线性分类器进行分类

Lecture 3 - Loss Function and Optmizatoin

目录