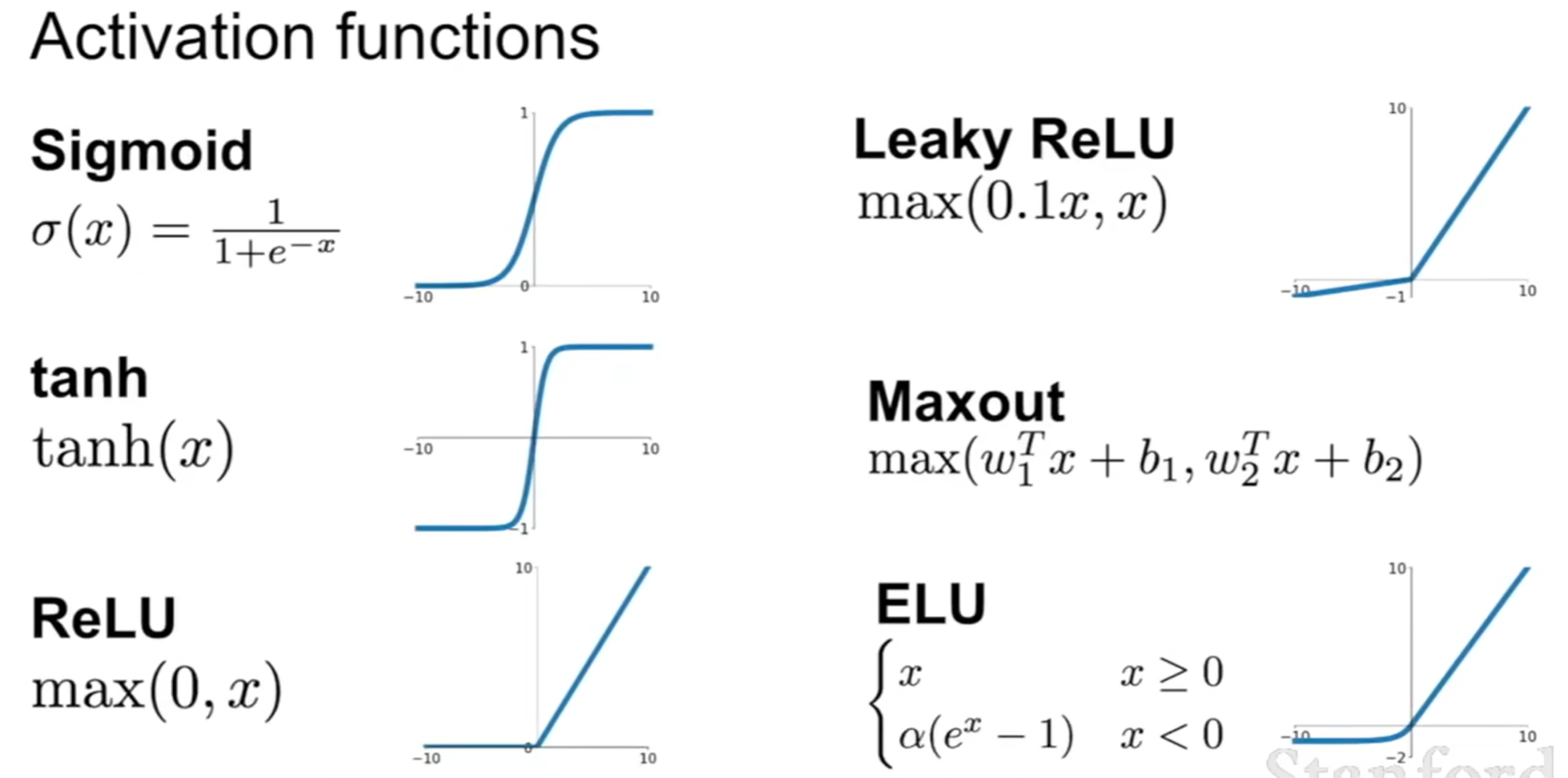
Lecture 4 - Backpropagation and Neural Networks

Backpropagation

Computational Graphs

• 以图的形式呈现计算过程，根据此计算过程，可以应用链式法则求解梯度

Backpropagation

• 计算图上的每一条链，都可以通过链式法则从后向前计算出前一个节点的梯度
• 使用这种方法，计算整体梯度被拆分成了计算若干个局部梯度，从而使得求解复杂函数的梯度变得可行

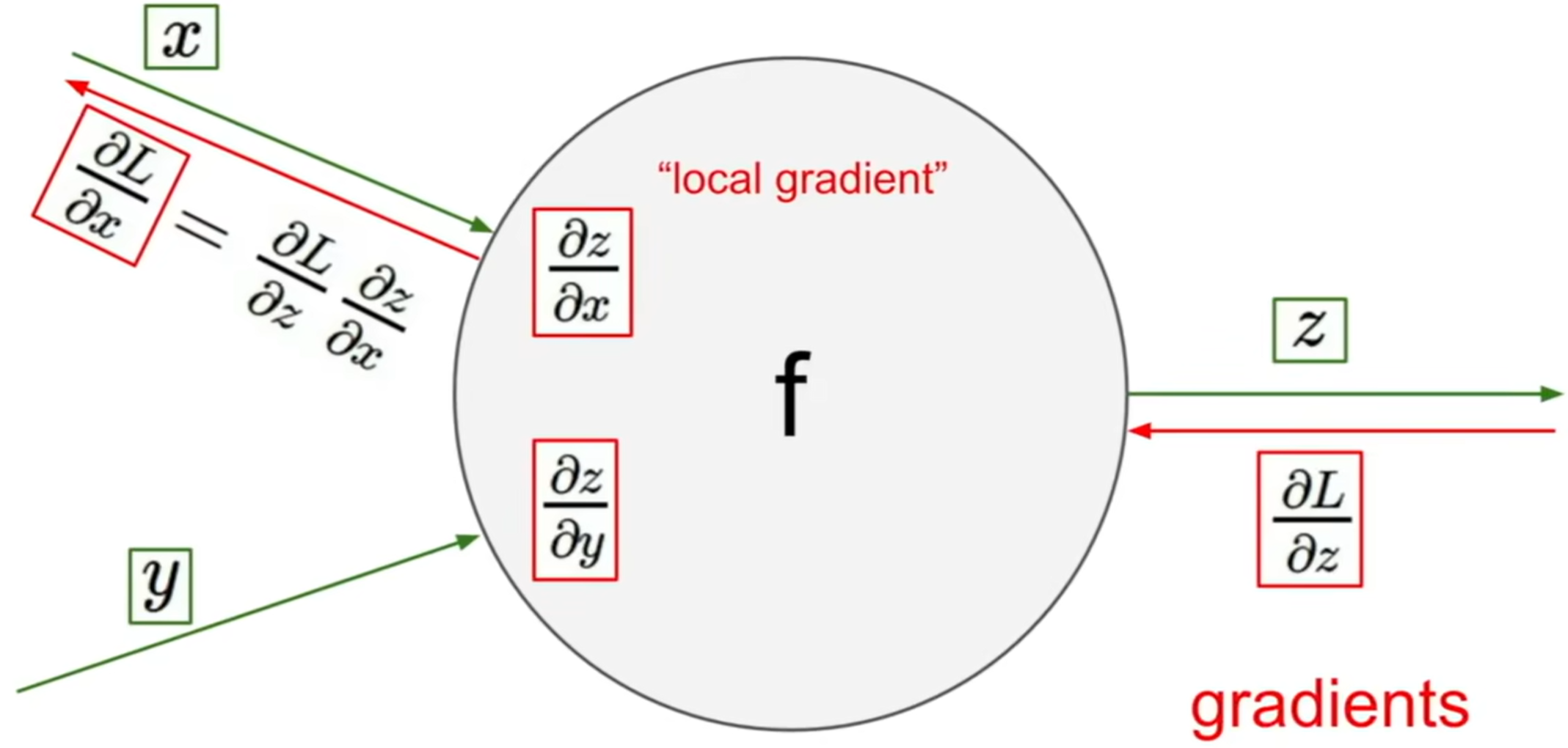
• 使用这种方法，我们可以将常用的函数的计算节点封装，从而实现直接调用，简化计算，例如：
  • Sigmoid Gate: $\sigma (x)={\displaystyle \frac{1}{1+e^{-x}}}$，由此可得到其梯度 ${\displaystyle \frac{\mathrm{d}\sigma (x)}{\mathrm{d}x}}=(1-\sigma (x))\sigma (x)$
  • Max Gate: 大的一方的局部梯度为 1，小的一方局部梯度为 0
• 不同的函数可以起到不同的作用：
  • Add Gate: gradient distributor，即 $f(x,y)=x+y$ 对两个变量的梯度都是 $1$，等价于直接将右边的梯度分别左传给坐标的两个变量
  • Max Gate: gradient router，即 $f(x,y)=max(x,y)$ 对大的梯度为 $1$，小的为 $0$，即大的一方获得全部梯度，小的没有任何梯度，等价于选择传入值大的一方赋予梯度
  • Mul Gate: gradient switcher，即 $f(x,y)=xy$ 对 $x$ 的梯度要乘上 $y$，对 $y$ 的梯度要乘上 $x$

Vectorized Operations

• 当输入为向量的时候，输出的偏导数就变成了雅可比矩阵，而雅可比矩阵的大小是输入向量维数×输出向量维数的，这就会导致计算非常的低效
• 在实际使用中，往往会对雅可比矩阵进行化简，直接找出右侧梯度输入和左侧变量输入与局部梯度的关系表达式，例如：
  • $f(\overrightarrow{x})=max(0,\overrightarrow{x})$，其对应的雅可比矩阵就是一个对角矩阵（因为输出的每一维只取决于输入的对应维）

• 若输入为矩阵 $A$，则对于矩阵的每一个位置，${\displaystyle \frac{\partial f_{\text{final}}}{\partial A_{ij}}}={\displaystyle \frac{\partial f_{\text{final}}}{\partial f_{\text{middle}}}}\times {\displaystyle \frac{\partial f_{\text{middle}}}{\partial A_{ij}}}$，因此，雅可比矩阵对应乘法是逐位相乘。

Neural Networks

• 通过线性层的相乘，组成更加复杂的非线性函数