Lecture 7 - Training Neural Networks

Fancier Optimization

SGD (Stochastic Gradient Descent）

• 某一维度的梯度移动可能很慢，导致了训练效率低下。例如，如果样本空间类似薯片形，则其在底部移动会非常慢
• 容易卡在局部最小值或者驻点，导致错误的结果或训练效率低下（梯度非常小，导致更新慢）
• 使用随机采样估计训练集整体的梯度，可能存在不准确的情况，也容易出现扰动

SGD + Momentum

• 引入"Momentum（动量）"的概念，将梯度作为加速度

• 其中 $\rho$ 是超参“动摩擦因子”，一般取值有 $0.9,0.99$，$\alpha$ 是超参 learning rate
• 这种方法可以有效解决 SGD 存在的问题：
  • 如果某一方向梯度太小但方向始终一致，$\rho v_t$ 项会使其梯度累加，即移动速度会逐渐增大
  • 因为“惯性”（即 $\rho v_t$ 项）的存在，不会卡在驻点，也不容易卡在局部最小值点上
  • 由于随机采样估计梯度产生的扰动的期望均值为 $0$，添加的 $\rho v_t$ 项可以有效抵消左右摆动，减少扰动，使得梯度下降的路径更加平滑

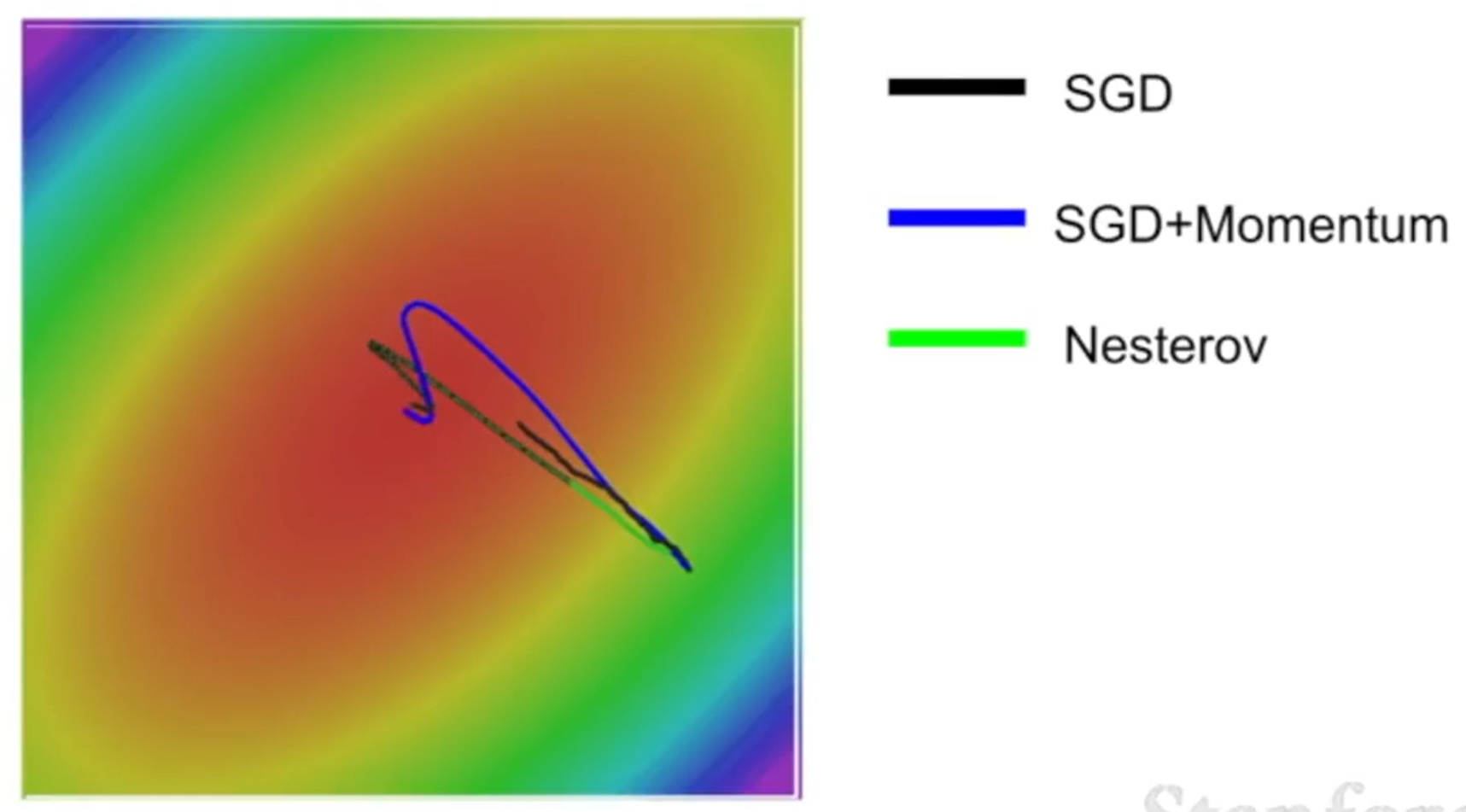
Nesterov Momentum

• 这样做可以使得更新方向更加接近估算梯度的方向
• 令 ${\tilde{x}}_t=x_t+\rho v_t$，则：

• 这个形式使得 Nesterov Momentum 可以有另一种解释：${\tilde{x}}_{t+1}$ 由旧的位置加上新的速度和乘上权重的纠偏构成

RMSProp

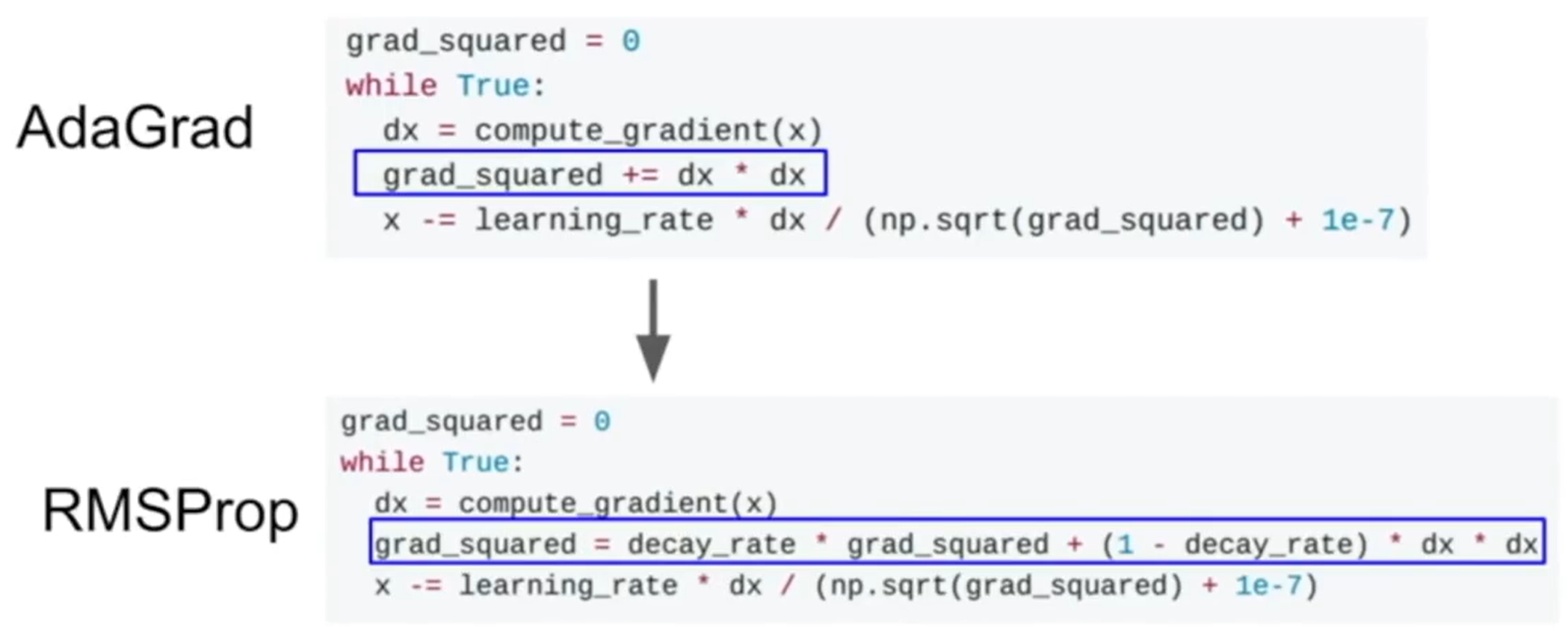
• 基本思路是通过累计标准差的形式，对每个维度的梯度进行放缩。如果在某个维度的梯度一直很小，则累计标准差也会很小，相除之后就会使得速度快起来。
• 为了防止除以 $0$ 的情况发生，一般会在分母加上一个 $1e7,1e8$ 之类的常数
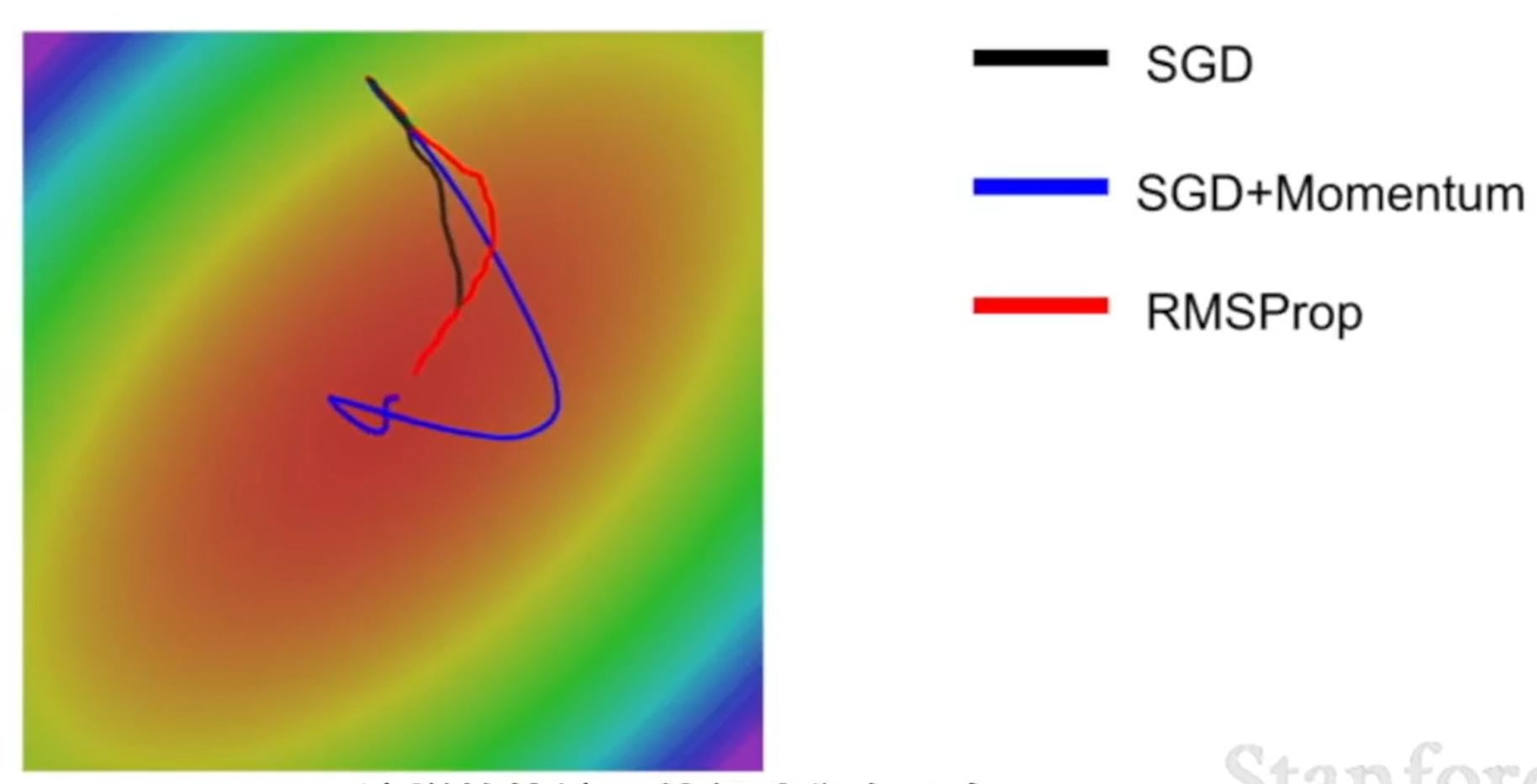
• 可以看到 RMSProp 可以以更加稳健的方式靠近结果

Adam

• 结合动量和标准差两种方法
• 通过偏差修正，避免第一步由于方差很小而产生的较大步长，从而使算法更加符合实际情况
• 通常设定超参数的取值为：beta1=0.9, beta2=0.999, learning rate=1e3 or 5e4

Second-Order Optimization

• 使用二阶近似的方式更新，这样就没有学习率参数了
• 但是这种方法在处理非凸问题和含有随机扰动的问题时效果不好，在参数过多的情况下，整体平方几乎不可能，故使用的不多

Regulazation

• Regulazation 的目的是为了增加模型的泛化能力，以尽量避免过拟合的发生

Dropout

• 每次前向传播时，随机地将每层的一部分神经元的输出设置为 0，即只使用部分神经元参与训练
• 一般对全连接层或卷积层进行操作

训练与预测

• 在训练时，网络变成了 $y=f(x,W,z)$，其中 $z$ 是随机生成的 mask
• 在预测时，我们不希望随机的 mask 影响到运行的结果，因此往往会采用采样平均的方式，即

Data Augmentation

• 通过使用随机混合、组合等方式，对数据进行变换，从而增加样本量和模型的泛用性，方法包括：
  • 变换
  • 旋转
  • 拉伸
  • 剪切
  • 畸变

Dropout Connection

• 不直接删除节点，而是随机删除某些连接关系

Fractional Max Pooling

• 输出的池化层是从多个池化层中随机选择合成的

Stochastic Depth

• 随机跳过某些层

Transfer Learning

• 在大样本数据集上训练的模型，通过一定方法，使其在垂直域上表现得更好